Like the absent Godot in Samuel Beckett's classic play Waiting for Godot, quantum computing is eagerly awaited—though no one is not quite sure when it will arrive or what it will do when it does. Quantum computing is rising on Gartner's hype cycle, so expectations are high — and likely to get even higher.
We are told that quantum computers will soon:
- Debug millions of lines of code in seconds
- Instantly break any contemporary encryption
Variations of the "break any contemporary encryption" prediction are the most common—and the most terrifying. Fortunately, they are likely wrong. Large universal quantum computers could break several popular public-key cryptography (PKC) systems, such as RSA and Diffie-Hellman, but that will not end encryption and privacy as we know it.
In the first place, it is unlikely that large-scale quantum computers will be built in the next several years. Second, alternative PKC systems already exist. Standards organizations and researchers are actively working to identify the best alternatives and plan the transition to post-quantum cryptography—cryptosystems that are secure against both classical and quantum computers and can work with existing communications protocols and networks.
Privacy is unlikely to die in a quantum apocalypse anytime soon. Here's why.
How security is quantified
The security of cryptography relies on certain "hard" problems—calculations that are practical to do with the right cryptographic key, but impractically difficult to do without it. A "hard" problem should take the best computers available billions of years to solve; an "easy" problem is one that can be solved very quickly.
The most widely used PKC systems, including RSA, Diffie-Hellman, and ECDSA, rely on the intractability of integer factorization and discrete log problems. These problems are hard for classical computers to solve, but easy for quantum computers.
This means that as soon as a large-scale universal quantum computer is built, you will not be able to rely on the security of any scheme based on these problems.
To quantify the security of cryptosystems, "bits of security" are used. You can think of this as a function of the number of steps needed to crack a system by the most efficient attack. A system with 112 bits of security would take 2112 steps to crack, which would take the best computers available today billions of years. Algorithms approved by NIST provide at least 112 bits of security.
The security of encryption depends on the length of the key and the cryptosystem used. A previous TechBeacon article explained the difference between quantum computers and classical computers, and described two quantum algorithms that will affect the security of cryptosystems.
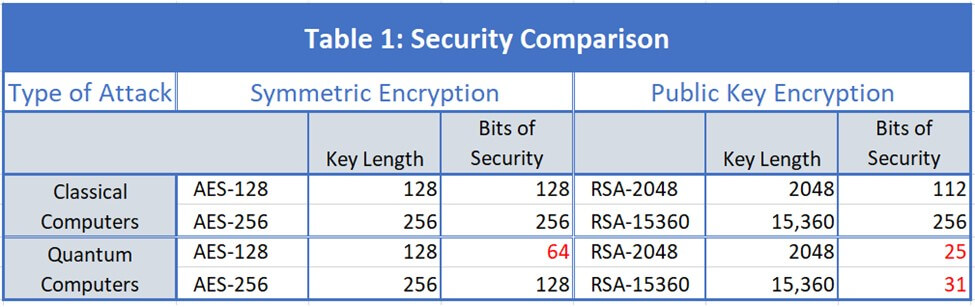
Shor's algorithm will be able to crack PKC systems like RSA and Diffie-Hellman; Grover's will reduce the security of symmetric cryptosystems like the Advanced Encryption Standard (AES), but not as drastically. Table 1 compares the security of both classical computers and quantum computers provided by AES and RSA.
AES-128 and RSA-2048 both provide adequate security against classical attacks, but not against quantum attacks. Doubling the AES key length to 256 results in an acceptable 128 bits of security, while increasing the RSA key by more than a factor of 7.5 has little effect against quantum attacks.
Post-quantum cryptography
When large-scale universal quantum computers are built, you will still be able to securely use symmetric encryption algorithms, but not the systems like RSA and Diffie-Hellman. These PKC systems are widely used today to create digital signatures or to securely transmit symmetric encryption keys.
Fortunately, there are several families of quantum-resistant PKC systems: Lattice-based, code-based, hash-based, isogeny-based, and multivariate systems. NIST's Report on Post-Quantum Cryptography describes each of these families.
Standards bodies are actively evaluating PKC systems from these families, looking for efficient algorithms with no known vulnerabilities to either classical or quantum attacks. IEEE and ANSI's X9 Committee have already specified standards for quantum-safe PKC schemes. ETSI and NIST have both issued reports on post-quantum cryptography, and NIST is currently evaluating 69 proposed schemes for U.S. government use.
The private sector is also making preparations. Examples of efforts underway range from Microsoft's PQC Project, through Open Quantum Safe's open source library of quantum safe algorithms, to QRL's quantum resistant cryptocurrency.
You obviously cannot accurately predict which systems are likely to be approved by NIST or any other standards organizations. But it does seem as if most of the effort is going into lattice-based, code-based, and hash-based systems, perhaps because these types of algorithms are more familiar.
Lattices are fundamentally important in optimization problems, so algorithms to solve lattice problems have been developed and studied for years. Code-based systems are based on error-correcting codes, which have also been extensively studied. And the security of hash-based signatures is well understood.
The 69 NIST submissions include 18 code-based and 21 lattice-based encryption candidates. Some of them have been around for years and appear to be secure against both quantum and classical attacks.
McEliece, for example, is a code-based encryption system developed in 1978; it has not been broken and it's listed as an approved primitive in the draft OASIS KMIP Post-Quantum Cryptography Profile. NTRU, a lattice-based encryption system developed in 1996, has already been approved for post-quantum use by IEEE and ANSI X9.
In the next three to five years, it is likely that NIST and other standards bodies will approve a few post-quantum systems, perhaps from different families, for PKC, key exchange, and digital signatures.
How long do we have?
Estimates of when large-scale quantum computers will be available vary widely. Developers of quantum computers say it will happen soon, while some researchers argue that we may never have the capability to build them. It is difficult for lay people to follow competing claims, as the definition of what constitutes a quantum computer may vary significantly from one vendor to the next.
For cryptographic purposes, though, we do know that cracking a 2048-bit RSA key will require thousands of entangled quantum bits (qubits). Entangled qubits form a single, very large state capable of doing the complex calculations needed to crack RSA. Entangling different kinds of qubits—photons, ions, or superconductors—is done with different processes. So far, no process seems to be more successful than the others.
The best results so far are:
- 18 fully entangled photon qubits in 2018
- 16 superconducting qubits, also in 2018
- 14 calcium ion qubits in 2011
Clearly there has been progress since the first pair of qubits was entangled in 1998, but it is not clear which process will scale best and no one has come close to the thousands of entangled qubits that will be needed to crack contemporary cryptosystems.
At this rate, RSA will not be cracked soon. Some researchers suggest five years; NIST thinks it may be 15. We'll see whose guess is closest eventually, but it seems fairly sure that there are at least a few years to prepare.
There's a software upgrade in your future
Preparation will involve developing quantum-safe algorithms for encryption and digital signatures that can be implemented in existing protocols and systems. Fundamentally, this is a software upgrade. No one likes software upgrades, though they are (too) often necessary.
Post-quantum cryptography will be a major change, but the industry has been through several significant cryptographic updates in the last 10 years: SHA-1, MD-5, RSA-1024, and Dual Elliptic Curve DRGB all had to be replaced by incompatible alternatives. Replacing RSA-2048 encryption with, for example, a suitable quantum-safe NTRU implementation would just be another such update.
Given the work already underway, researchers should be able to implement quantum-safe cryptography well before large-scale quantum computers are available to break RSA.
Keep learning
Get up to speed on unstructured data security with TechBeacon's Guide. Plus: Get the Forrester Wave for Unstructured Data Security Flatforms, Q2 2021.
Join this discussion about how to break the Ground Hog Day repetition with better data management capabilities.
Learn how to accelerate your analytics securely into the cloud in this Webinar.
Find out more about cloud security and privacy, and selecting the right encryption and key management in TechBeacon's Guide.
Learn to appreciate the art of data protection and go behind the privacy shield in this Webinar.
Dive into the new laws with TechBeacon's guide to GDPR and CCPA.